Ecuaciones trascendentes y diferenciales
Ecuaciones trascendentes
Una ecuación trascendente es una igualdad entre dos expresiones matemáticas en las que aparecen una o más incógnitas relacionadas mediante operaciones matemáticas, que no son únicamente algebraicas, y cuya solución no puede obtenerse empleando solo las herramientas propias del álgebra.
Ecuaciones exponenciales propiedades
En esta sección vamos a ver los casos en que se pueden presentar las ecuaciones exponenciales y que recomendación debemos seguir para la resolución de los ejercicios.
Cuando tengamos ejercicios de ecuaciones exponenciales de igual base la ecuación la formaremos igualando los exponentes.
Ecuaciones diferenciales
Una ecuación diferencial es una ecuación matemática que relaciona una función con sus derivadas. En las matemáticas aplicadas, las funciones usualmente representan cantidades físicas, las derivadas representan sus razones de cambio, y la ecuación define la relación entre ellas.
Ejemplos:
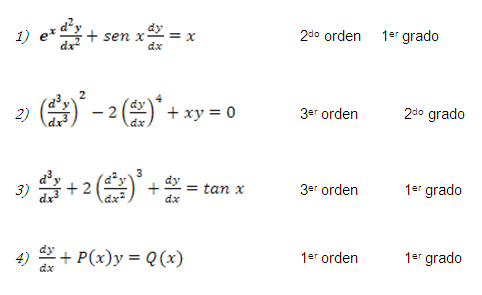
Una ecuación trascendente es una igualdad entre dos expresiones matemáticas en las que aparecen una o más incógnitas relacionadas mediante operaciones matemáticas, que no son únicamente algebraicas, y cuya solución no puede obtenerse empleando solo las herramientas propias del álgebra.
Ecuaciones Trascendentes características
Las características principales en este tipo de ejercicios son:- Se presenta una ecuación con una variable, pero en ambos miembros existen bases y exponentes.
- Las bases de estas ecuaciones en su mayoría de veces las podemos igualar. Se puede reducir de tal forma que conseguiremos que sean iguales
- Si las bases no pueden ser iguales, lo exponentes serán quienes cumplan esta función.
- Ecuaciones Exponenciales teoría
- Son aquellos cuya incógnita figura en el exponente o en la base. Se estudian aquellos casos cuya solución es factible gracias a la utilización de las leyes de la teoría de exponentes.
En esta sección vamos a ver los casos en que se pueden presentar las ecuaciones exponenciales y que recomendación debemos seguir para la resolución de los ejercicios.
Primer caso:
Bases iguales.
Cuando tengamos ejercicios de ecuaciones exponenciales de igual base la ecuación la formaremos igualando los exponentes.
Ecuaciones diferenciales
Una ecuación diferencial es una ecuación matemática que relaciona una función con sus derivadas. En las matemáticas aplicadas, las funciones usualmente representan cantidades físicas, las derivadas representan sus razones de cambio, y la ecuación define la relación entre ellas.
Ejemplos:
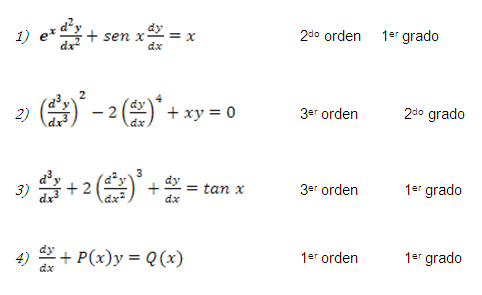


No hay comentarios.:
Publicar un comentario